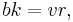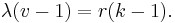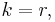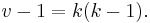Block design

In combinatorial mathematics, a block design is a set together with a family of subsets (repeated subsets are allowed at times) whose members are chosen to satisfy some set of properties that are deemed useful for a particular application. These applications come from many areas, including experimental design, finite geometry, software testing, cryptography, and algebraic geometry. Many variations have been examined, but the most intensely studied are the balanced incomplete block designs (BIBDs or 2-designs) which historically were related to statistical issues in the design of experiments.^[1]^[2]

1 Definition of a BIBD
2 Examples
- 2.1 Projective planes
- 2.2 Biplanes
3 Generalization: t-designs
- 3.1 Derived and extendable t-designs
  - 3.1.1 Geometric examples
4 Pairwise balanced designs
5 See also
6 Notes
7 References
8 External links

Definition of a BIBD

Given a finite set X (of elements called points) and integers k, r, λ ≥ 1, we define a 2-design (or BIBD, standing for balanced incomplete block design) B to be a family of k-element subsets of X, called blocks, such that the number r of blocks containing x in X is independent of x, and the number λ of blocks containing given distinct points x and y in X is also independent of the choices.

"Family" in the above definition can be replaced by "set" if repeated blocks are not allowed. Designs in which repeated blocks are not allowed are called simple.

Here v (the number of elements of X, called points), b (the number of blocks), k, r, and λ are the parameters of the design. (To avoid degenerate examples, it is also assumed that v > k, so that no block contains all the elements of the set. This is the meaning of "incomplete" in the name of these designs.) In a table:

v	points, number of elements of X
b	blocks
r	number of blocks containing a given point
k	number of points in a block
λ	number of blocks containing 2 (or more generally t) points

The design is called a (v, k, λ)-design or a (v, b, r, k, λ)-design. The parameters are not all independent; v, k, and λ determine b and r, and not all combinations of v, k, and λ are possible. The two basic equations connecting these parameters are

$bk = vr, \,$

$\lambda(v-1) = r(k-1). \,$

These conditions are not sufficient as, for example, a (43,7,1)-design does not exist.^[3]

The order of a 2-design is defined to be n = r - λ.

A fundamental theorem, Fisher's inequality, named after Ronald Fisher, is that b ≥ v in any 2-design. In the case of equality, the 2-design is called a symmetric design^[4]; it has many special features. In a symmetric design r = k holds as well as b = v, and, while it is generally not true in arbitrary 2-designs, in a symmetric design every two distinct blocks meet in λ points.

Examples

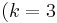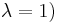A block design in which all the blocks have the same size is called uniform. Examples of uniform block designs include finite projective planes (where X is the set of points of the plane and λ = 1), and Steiner triple systems $(k = 3$ and $\lambda=1)$ . The former is a relatively simple example of a symmetric design. Triple systems $(k=3)$ are of interest in their own right.^[5] Examples of block designs that are not uniform are given by Pairwise block designs (PBD's).

Projective planes

Main article: Projective plane

Finite projective planes are symmetric 2-designs with λ = 1 and order n > 1. Since these designs are symmetric, it follows from the first basic equation that

$k = r, \,$

and since 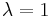$\lambda = 1$ by definition, the second equation gives us

$v-1 = k(k-1).\,$

Since k = r we can write the order of a projective plane as n = k - 1 and, from the displayed equation above, we have 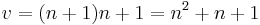$v = (n%2B1)n %2B 1 = n^2 %2B n %2B 1$ points in a projective plane of order n.

Since a projective plane is symmetric, we have that 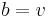$b = v$ , which means that 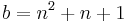$b = n^2 %2B n %2B 1$ also. The number b is the number of lines of the projective plane. Since λ = 1 there can be no repeated lines, so a projective plane is a simple 2-design in which the number of lines and the number of points are always the same. For a projective plane, k is the number of points on each line and it is equal to n + 1. Similarly, r = n + 1 is the number of lines with which a given point is incident.

For n = 2 we get a projective plane of order 2, also called the Fano plane, with v = 4 + 2 + 1 = 7 points and 7 lines. In the Fano plane, each line has n + 1 = 3 points and each point belongs to n + 1 = 3 lines.

Biplanes

A biplane or biplane geometry is a symmetric design ("projective" or "square" design), with λ = 2 – any set of two points is contained in two blocks ("lines"), while any two lines intersect in two points.^[6] They are similar to finite projective planes, except that rather than two points determining one line (and two lines determining one point), two points determine two lines (respectively, points). A biplane of order n is one whose blocks have 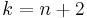$k=n%2B2$ points, and has 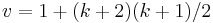$v=1%2B(k%2B2)(k%2B1)/2$ points (since $r=k$ ).

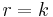As examples:^[7]

(Trivial) The order 0 biplane has 2 points (and lines of size 2 – (2,2,2)); it is two points, with two blocks, each consisting of both points. Geometrically, it is the digon.

One can also define trivial biplanes of order −1 (1 point, lines of size 1 (2,1,2) – the point is contained in the line) and −2 (1 point, lines of size 0 (2,0,2) – the point is not contained in the line).

The order 1 biplane has 4 points (and lines of size 3 – (4,3,2)); it is the complete design with v = 4 and k = 3. Geometrically, the points are the vertices and the blocks are the faces of a tetrahedron.
The order 2 biplane is the complement of the Fano plane: it has 7 points (and lines of size 4 – (7,4,2)), where the lines are given as the complements of the (3-point) lines in the Fano plane.^[8]
The order 3 biplane has 11 points (and lines of size 5 – (11,5,2)), and is also known as the Paley biplane after Raymond Paley; it is associated to the Paley digraph of order 11, which is constructed using the field with 11 elements, and is associated to the order 12 Hadamard matrix; see Paley construction I.

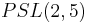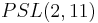Algebraically this corresponds to the exceptional embedding of the projective special linear group $PSL(2,5)$ in $PSL(2,11)$ – see projective linear group: action on p points for details.^[8]

There are three biplanes of order 4 (16 points, lines of size 6 – (16,6,2)).
There are five biplanes of order 9 (and 56 points, lines of size 11 – (56,11,2)).^[9]

Generalization: t-designs

Given any integer t ≥ 2, a t-design B is a class of k-element subsets of X, called blocks, such that every point x in X appears in exactly r blocks, and every t-element subset T appears in exactly λ blocks. The numbers v (the number of elements of X), b (the number of blocks), k, r, λ, and t are the parameters of the design. The design may be called a t-(v,k,λ)-design. Again, these four numbers determine b and r and the four numbers themselves cannot be chosen arbitrarily. The equations are

$b_i = \lambda \left.\binom{v-i}{t-i} \right/ \binom{k-i}{t-i} \text{ for } i = 0,1,\ldots,t,$

where b_i is the number of blocks that contain any i-element set of points.

There are no known examples of non-trivial t-(v,k,1)-designs with 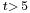$\scriptstyle t >\, 5$ .

The term block design by itself usually means a 2-design.

Derived and extendable t-designs

Let D = (X, B) be a t-(v,k,λ) design and p a point of X. The derived design D_p has point set X - {p} and as block set all the blocks of D which contain p with p removed. It is a (t-1)- (v-1, k-1, λ) design. Note that derived designs with respect to different points may not be isomorphic. A design E is called an extension of D if E has a point p such that E_p is isomorphic to D; we call D extendable if it has an extension.

If a t-(v,k,λ) design has an extension, then k+1 divides b(v+1).

The only extendable projective planes (symmetric 2-(n²+n+1, n+1, 1) designs) are those of orders 2 and 4.

A design with the parameters of the extension of an affine plane, i.e., a 3-(n² + 1, n+1,1) design, is called a finite inversive plane, or a Möbius plane of order n.

Geometric examples

It is possible to give a geometric description of some inversive planes. An ovoid in PG(3,q) is a set of q² + 1 points, no three collinear. It can be shown that every plane (which is a hyperplane since the geometric dimension is 3) of PG(3,q) meets an ovoid O in either 1 or q + 1 points. The plane sections of size q + 1 of O are the blocks of an inversive plane of order q. Any inversive plane arising this way is called egglike. All known inversive planes are egglike.

An example of an ovoid is the elliptic quadric, the set of zeros of the quadratic form

x₁x₂ + f(x₃, x₄),

where f is an irreducible quadratic form in two variables over GF(q). [f(x,y) = x² + xy + y² for example].

If q is an odd power of 2, another type of ovoid is known - the Suzuki-Tits ovoid.

Theorem. (a) If q is odd, then any ovoid is projectively equivalent to the elliptic quadric; so there is a unique egglike inversive plane of order q (but it is unknown if non-egglike ones exist). (b) if q is even, then any inversive plane is egglike (but there maybe some unknown ovoids).

Pairwise balanced designs

A pairwise balanced design (or PBD) is a set X together with a family of subsets of X (which need not have the same size and may contain repeats) such that every pair of distinct elements of X is contained in exactly λ (a positive integer) subsets. The set X is allowed to be one of the subsets, and if all the subsets are copies of X, th PBD is called trivial. The size of X is v and the number of subsets in the family (counted with multiplicity) is b.

Fisher's inequality holds for PBDs.

Theorem: For any non-trivial PBD, v ≤ b.^[10]

This result also generalizes the famous Erdős-De Bruijn theorem :

For a PBD with λ = 1 having no blocks of size 1 or size v, v ≤ b, with equality if and only if the PBD is a projective plane or a near-pencil. ^[11]

Notes

^ Handbook of combinatorial designs. Edited by Charles J. Colbourn and Jeffrey H. Dinitz. Second edition. Discrete Mathematics and its Applications (Boca Raton). Chapman & Hall/CRC, Boca Raton, FL, 2007
^ Stinson, Douglas R. Combinatorial designs: Constructions and analysis. Springer-Verlag, New York, 2004. xvi+300 pp. ISBN 0-387-95487-2
^ Proved by Tarry in 1900 who showed that there was no pair of orthogonal Latin squares of order six. The 2-design with the indicate parameters is equivalent to the existence of five mutually orthogonal Latin squares of order six.
^ There have been several attempts to change the terminology because there is no "symmetry" in the usual sense of that term in these designs. "Projective designs" had been suggested by P.Dembowski (1968) in Finite Geometries and "Square designs" had been suggested by P.J. Cameron and J.H. van Lint (1991) in Designs, Graphs, Codes and their Links.
^ Colbourn, Charles J. and Rosa, Alexander, Triple systems, Oxford Mathematical Monographs,The Clarendon Press Oxford University Press, New York.1999,ISBN 0-19-853576-7
^ ATLAS of Finite Groups, p. 7
^ Designs and their codes, by E. F. Assmus, J. D. Key, p. 126
^ ^a ^b Martin, Pablo; Singerman, David (April 17, 2008), From Biplanes to the Klein quartic and the Buckyball, p. 4, http://www.neverendingbooks.org/DATA/biplanesingerman.pdf
^ Kaski, Petteri and Östergård, Patric (2008). "There Are Exactly Five Biplanes with k = 11". Journal of Combinatorial Designs 16 (2): 117–127. doi:10.1002/jcd.20145. MR 2008m:05038.
^ Stinson 2003, pg.193
^ Stinson 2003, pg.183

References

R. C. Bose, "A Note on Fisher's Inequality for Balanced Incomplete Block Designs", Annals of Mathematical Statistics, 1949, pages 619–620.

R. A. Fisher, "An examination of the different possible solutions of a problem in incomplete blocks", Annals of Eugenics, volume 10, 1940, pages 52–75.

Raghavarao, Damaraju (1988). Constructions and Combinatorial Problems in Design of Experiments (corrected reprint of the 1971 Wiley ed.). New York: Dover.

Raghavarao, Damaraju and Padgett, L.V. (2005). Block Designs: Analysis, Combinatorics and Applications. World Scientific.

S. S. Shrikhande, and Vasanti N. Bhat-Nayak, Non-isomorphic solutions of some balanced incomplete block designs I – Journal of Combinatorial Theory, 1970

Stinson, Douglas R. (2003), Combinatorial Designs: Constructions and Analysis, New York: Springer, ISBN 0-387-95487-2

Street, Anne Penfold and Street, Deborah J. (1987). Combinatorics of Experimental Design. Oxford U. P. [Clarendon]. pp. 400+xiv. ISBN 0198532563.

van Lint, J.H., and R.M. Wilson (1992), A Course in Combinatorics. Cambridge, Eng.: Cambridge University Press.

External links

Design DB: A database of combinatorial, statistical, experimental block designs

Weisstein, Eric W., "Block Designs" from MathWorld.

Design of experiments

Scientific Method	Scientific experiment · Statistical design · Control · Internal & external validity · Experimental unit · Blinding Optimal design: Bayesian · Random assignment · Randomization · Restricted randomization · Replication versus subsampling · Sample size

Treatment & Blocking	Treatment · Effect size · Contrast · Interaction · Confounding · Orthogonality · Blocking · Covariate · Nuisance variable

Models & Inference	Linear regression · Ordinary least squares · Bayesian Random effect · Mixed model · Hierarchical model: Bayesian Analysis of variance (Anova) · Cochran's theorem · Manova (multivariate) · Ancova (covariance) Compare means · Multiple comparison

Designs: Completely Randomized	Factorial · Fractional factorial · Plackett-Burman · Taguchi Response surface methodology · Polynomial & rational modeling · Box-Behnken · Central composite Block · Generalized randomized block design (GRBD) · Latin square · Graeco-Latin square · Hyper-Graeco-Latin square · Latin hypercube Repeated measures design · Crossover study · Randomized controlled trial · Sequential analysis · Sequential probability ratio test

Glossary · Category · Statistics portal · Statistical outline · Statistical topics